- 1. Why does randomness matter for cybersecurity?
- 2. How do quantum random number generators actually work?
- 3. What makes quantum randomness different from classical randomness?
- 4. What types of QRNGs exist today?
- 5. How is quantum randomness tested and certified?
- 6. Where are quantum random number generators being used today?
- 7. What are the current challenges with QRNGs?
- 8. Where is QRNG technology heading next?
- 9. QRNG FAQs
- Why does randomness matter for cybersecurity?
- How do quantum random number generators actually work?
- What makes quantum randomness different from classical randomness?
- What types of QRNGs exist today?
- How is quantum randomness tested and certified?
- Where are quantum random number generators being used today?
- What are the current challenges with QRNGs?
- Where is QRNG technology heading next?
- QRNG FAQs
What Is a Quantum Random Number Generator (QRNG)? Overview
- Why does randomness matter for cybersecurity?
- How do quantum random number generators actually work?
- What makes quantum randomness different from classical randomness?
- What types of QRNGs exist today?
- How is quantum randomness tested and certified?
- Where are quantum random number generators being used today?
- What are the current challenges with QRNGs?
- Where is QRNG technology heading next?
- QRNG FAQs
A quantum random number generator is a device that uses quantum mechanical processes to produce truly random numbers. It relies on unpredictable quantum events, such as measurement outcomes of quantum states, as a source of entropy.
Unlike algorithmic generators that only simulate randomness, a QRNG measures it directly from physical phenomena that cannot be predicted or repeated.
Why does randomness matter for cybersecurity?
Randomness matters for cybersecurity because it's what prevents encrypted systems from being predictable or reversible.
More specifically:
Every modern encryption system depends on randomness.
Keys, tokens, and initialization vectors all start with numbers that no one should be able to guess. That randomness is what keeps encrypted data secure. If an attacker can predict how a key was generated, the entire system can be broken.
Most systems today use pseudo-random number generators.
They rely on algorithms that produce numbers that look random but aren't truly unpredictable. If someone discovers the algorithm or its initial seed, they can reproduce every “random” value that follows. In other words, the randomness wasn't random—it was math.
That predictability creates weak points in encryption.
It's happened before: flawed random generators have led to broken keys, compromised certificates, and decrypted traffic. Even small entropy failures, where randomness becomes predictable or biased, can expose large systems.
To give further context, entropy is a measure of unpredictability.
The higher the entropy, the stronger the key. Low entropy means patterns that attackers can find and exploit.
This is where quantum random number generators change the equation. They draw entropy from quantum events that can't be predicted or replicated. Which means the randomness is rooted in physics, not software.
In Zero Trust and post-quantum security models, that matters.
Organizations are moving toward architectures where nothing is implicitly trusted—not users, not devices, and not encryption keys. So using quantum randomness helps ensure the foundation of those keys stays unguessable, even in a future where quantum computers exist.
In short, if randomness fails, encryption fails. Quantum randomness is designed to make sure it never does.
How do quantum random number generators actually work?
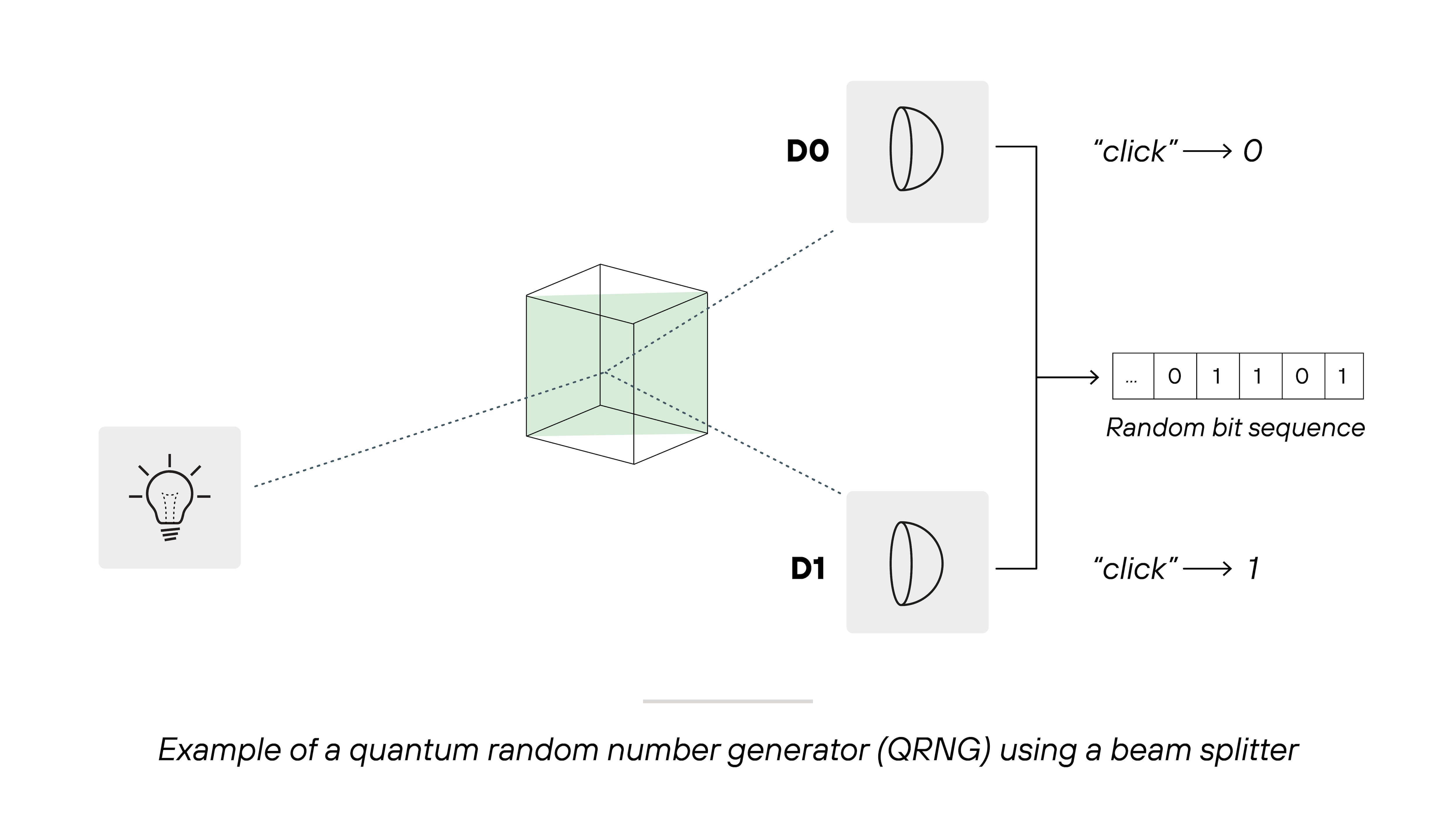
A quantum random number generator creates randomness by observing unpredictable events in nature. Instead of running an algorithm, it measures quantum behavior that cannot be forecast or repeated.
At a high level, every QRNG follows the same sequence of steps: generate a quantum event → measure its outcome → convert it into digital form → and verify that the result meets strict statistical standards. Each stage ensures the randomness is both physically genuine and cryptographically usable.
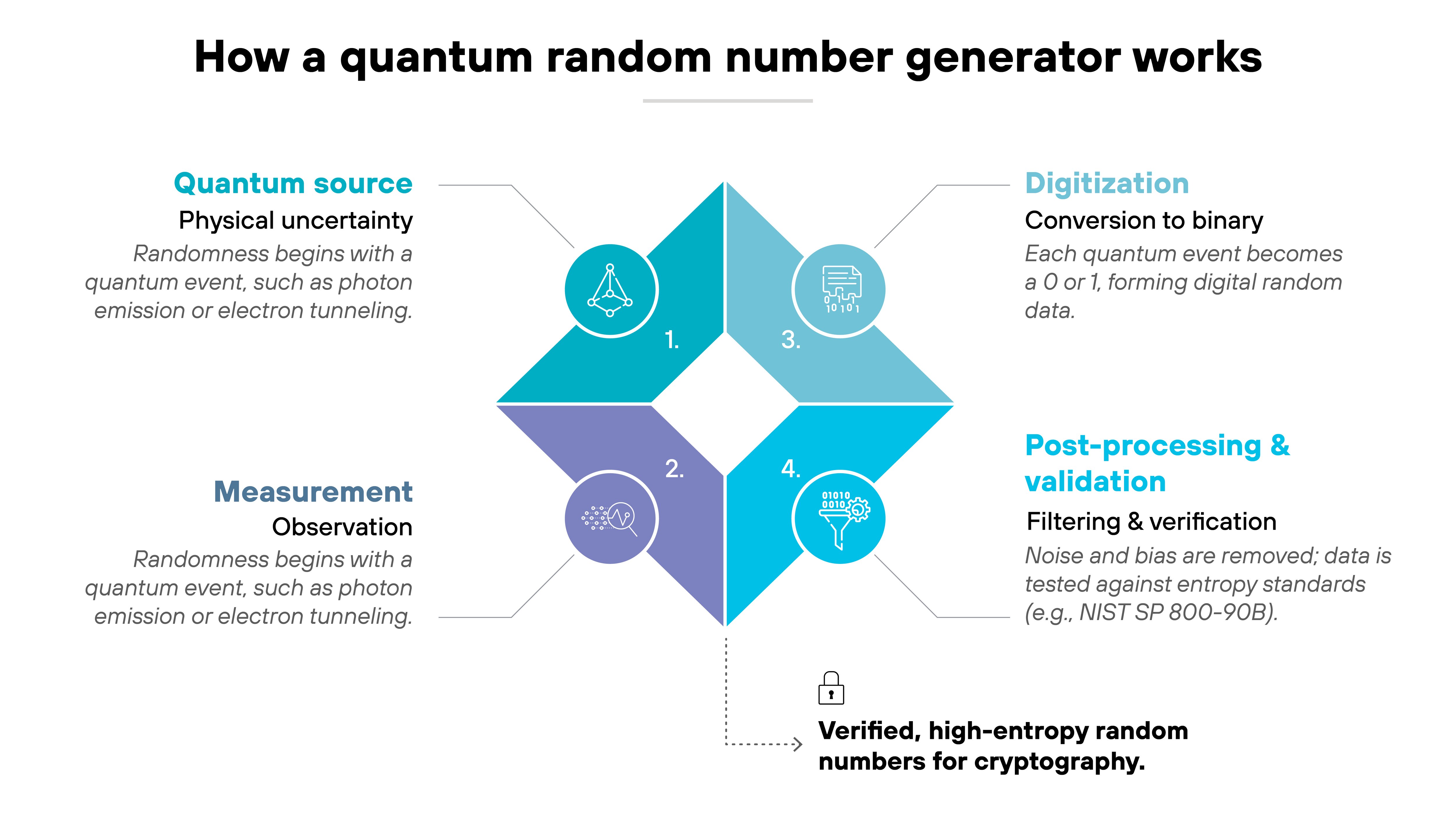
Here's how the process works:
-
Quantum source
Every QRNG begins with a quantum process that produces true physical uncertainty.
Common examples include light particles, electron tunneling, or tiny energy fluctuations that exist even in empty space. These sources generate raw randomness at the hardware level before any computation takes place.
-
Measurement
Detectors record outcomes from that quantum process, such as which path a photon takes, when it arrives, or how its energy changes.
Each outcome is genuinely unpredictable. The system collects many of these measurements to build a stream of random events.
-
Digitization
Those random events are then converted into binary form. Each detection becomes a 0 or a 1.
This translation turns physical measurements into digital data that can be used in computing and cryptography. However, electronic components can introduce minor bias or noise, so the data still needs refinement.
-
Post-processing and validation
In the final step, the QRNG filters noise, removes bias, and tests the data's statistical quality.
The output must meet entropy and uniformity thresholds defined in standards such as NIST SP 800-90B. The post-processing algorithms themselves are deterministic, but they operate only on data that has been verified to come from a quantum source.
These checks confirm that the randomness originates from quantum physics, not from deterministic or classical effects.
The result is verified, high-entropy randomness suitable for secure key generation and cryptographic applications. Essentially, QRNGs don't simulate randomness. They measure it directly from the most unpredictable systems known.
What makes quantum randomness different from classical randomness?
Classical random number generators rely on predictable processes.
Some use algorithms that create sequences which only appear random. Others use physical noise, like electrical fluctuations, but still depend on measurable factors that can be modeled or repeated.
Quantum random number generators work differently.
They draw randomness from quantum physics itself, where outcomes truly have no predetermined cause. That makes the results irreproducible, even if every initial condition is known.
Here's how the two compare:
| Comparison: Classical vs. quantum randomness |
|---|
| Feature | Classical RNG | Quantum RNG |
|---|---|---|
| Source | Algorithmic or physical | Quantum phenomena |
| Predictability | Deterministic if seed known | Fundamentally unpredictable |
| Repeatability | Repeatable | Irreproducible |
| Security | Vulnerable to modeling | Certified true randomness |
To break it down: classical randomness is simulated. Quantum randomness is observed.
That distinction matters.
A classical generator can always, in theory, be reverse-engineered if someone discovers its logic or starting seed. A quantum generator, by contrast, measures randomness directly from nature. Not from a model of it. Which means its results can't be replicated, predicted, or guessed.
What types of QRNGs exist today?

Quantum random number generators differ mainly in how they trust and verify their hardware.
Each type uses quantum principles to generate entropy but balances speed, security, and proof differently.
Here's how they compare.
Trusted-device QRNGs
These are the simplest and fastest systems. They assume that both the quantum source and detectors are functioning as intended.
Because they trust the hardware entirely, they don't require extra verification steps.
Trusted-device designs are common in commercial products where throughput and simplicity matter most.
Device-independent QRNGs
Device-independent QRNG systems take the opposite approach.
They don't assume any part of the hardware is honest. Instead, they rely on loophole-free Bell tests. Which are experiments that prove randomness through quantum entanglement. That makes them the most verifiable, but also the slowest and most complex to build.
They're mostly found in research and high-assurance applications that prioritize proof over performance.
Source-independent QRNGs
These offer a middle ground. They trust only the detectors, not the quantum source.
This allows for partial verification while maintaining good performance.
Source-independent systems can still guarantee quantum-origin randomness without the heavy overhead of full device independence.
Integrated or chip-based QRNGs
This is the newest category.
Integrated designs use silicon photonics or CMOS components to embed QRNG functions directly on a chip. They're smaller, faster, and more energy efficient.
That makes them practical for mobile devices, IoT hardware, and large-scale data centers.
Together, these approaches show how QRNGs are evolving from specialized lab systems into scalable, deployable components for real-world security infrastructure. While QRNGs are still emerging compared to post-quantum cryptography, they're definitely moving from research prototypes to practical components within security infrastructure.
How is quantum randomness tested and certified?
Randomness in quantum systems isn't assumed. It's tested, verified, and certified before it's used in cryptography or scientific research.
That validation process focuses on confirming that the randomness truly comes from a quantum source. Not from hardware noise or software artifacts.
Statistical tests evaluate the outcomes, while entropy validation examines the source itself. That distinction matters because both must hold up before a QRNG can be considered trustworthy.

Testing starts with statistical analysis.
Frameworks like NIST SP 800-22 apply a suite of tests to evaluate bit sequences for patterns. They measure whether the data is uniform, unbiased, and unpredictable across large samples.
But statistical tests alone can't prove where the randomness came from.
That's why NIST SP 800-90B adds entropy validation. It checks the quality of the entropy source itself—detecting bias, verifying independence between bits, and confirming that outputs remain stable under varying operating conditions.
Certified randomness goes further. It means the results are provably unpredictable even if every part of the system is known.
Device-independent QRNGs achieve this through physical principles such as Bell-test correlations, showing that the randomness is quantum in origin and not produced by classical processes.
The Colorado University Randomness Beacon (CURBy), created by the University of Colorado Boulder in collaboration with NIST, represents a major step in making that kind of verified randomness publicly accessible.
It combines NIST's Bell-test–based entangled-photon source with CU Boulder's Twine protocol, which is a blockchain-style verification system that traces and audits every random value produced.
Together, they built the first public quantum randomness beacon. One that continuously broadcasts certified random numbers that anyone can inspect, use, and verify.
The key point is that randomness certification turns a physical process into mathematical assurance. It's how organizations can trust that quantum-generated numbers are genuinely unpredictable. And safe to use as the foundation of secure systems.
Where are quantum random number generators being used today?

Quantum random number generators are moving from research environments into production systems. They're being deployed in environments where provable randomness strengthens trust, transparency, and cryptographic assurance.
QRNG adoption is growing across sectors that depend on entropy quality. From secure communications and cryptographic infrastructure to scientific research and public verification systems.
Here's where they're already making an impact:
-
Cryptographic key generation
This is the core use case. QRNGs feed entropy directly into key generation systems for encryption, digital signatures, and secure authentication tokens.
Because the randomness comes from quantum phenomena, the resulting keys are unpredictable. Even to someone who understands hardware design.
-
Secure communications
Modern VPNs, TLS, and post-quantum cryptographic systems increasingly draw entropy from QRNGs. Each session begins with a seed that's physically random, closing gaps left by traditional pseudo-random generators.
That makes encryption handshakes and session keys harder to predict or reuse.
-
Scientific simulations
Quantum randomness is also valuable outside cybersecurity. In research, finance, and AI, simulations often rely on random inputs to model uncertainty.
Using quantum-generated randomness improves statistical precision and minimizes bias in those models.
-
Public randomness beacons
Initiatives like NIST's CURBy beacon publish quantum-verified random numbers to the public.
They're used to ensure fairness and transparency in lotteries, audits, and other processes where trust must be mathematically provable. Because the output is verifiable, anyone can confirm that results weren't influenced or altered.
Across all these applications, QRNGs support quantum readiness. They strengthen Zero Trust architectures by ensuring that every key, session, or model begins with entropy that's genuinely unpredictable. Not algorithmically simulated.
What are the current challenges with QRNGs?
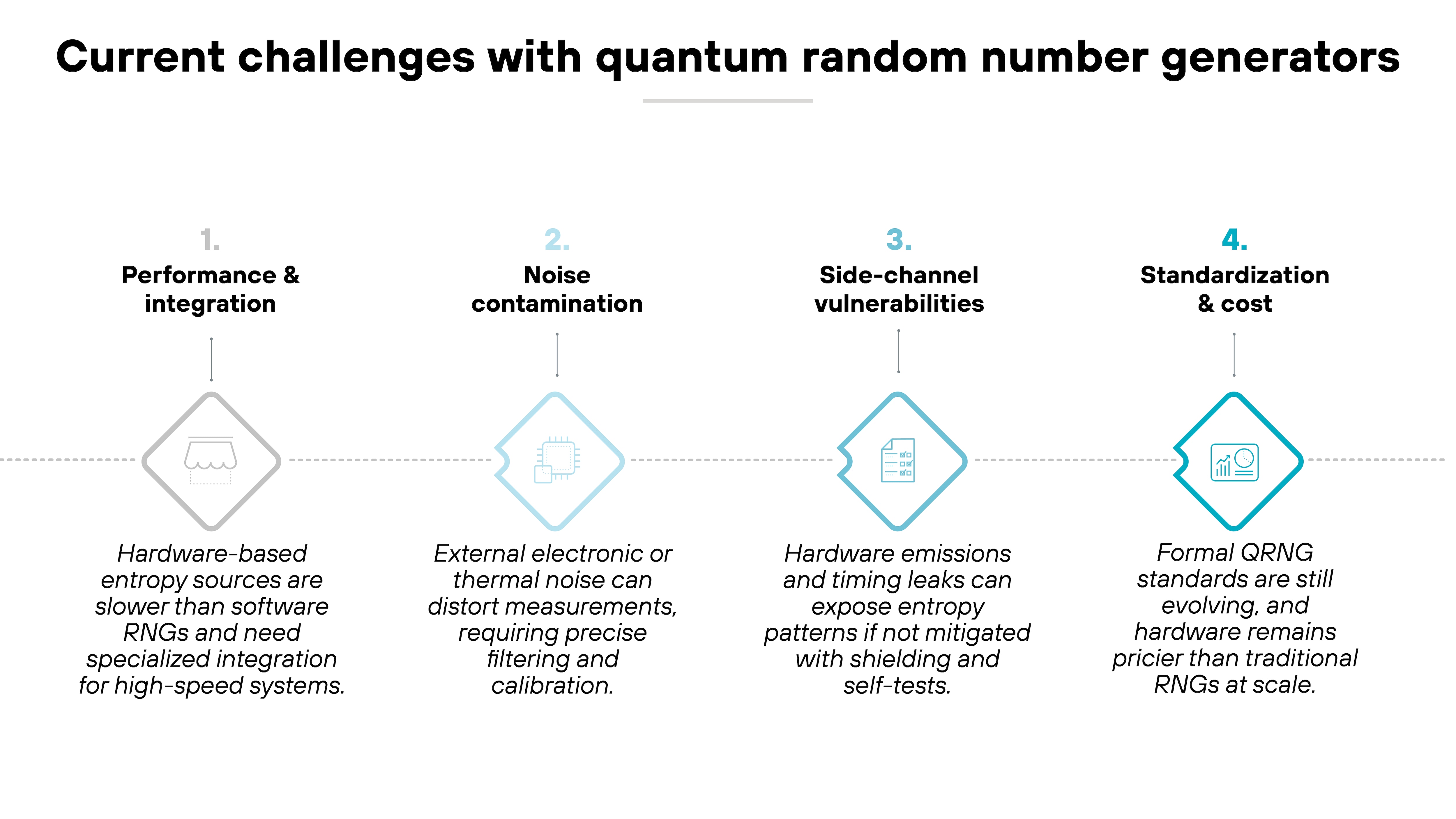
Quantum random number generators are advancing quickly, but they still face several practical challenges before reaching mainstream deployment.
These issues reflect ongoing engineering work. Not fundamental limitations of quantum randomness itself.
Performance and integration remain top considerations.
QRNGs are typically slower than pseudo-random generators, especially when implemented with optical hardware or entropy verification. Throughput continues to improve as chip-based and hybrid designs become more efficient. But integration into high-speed systems still takes specialized engineering.
Noise contamination can also affect output quality.
Quantum entropy sources are sensitive, and external electronic or thermal noise can distort measurements. Advanced filtering and calibration reduce that risk, but maintaining clear separation between classical and quantum noise remains a design priority.
Side-channel vulnerabilities have become a new research focus.
Machine learning-based cryptanalysis has shown that hardware emissions and timing patterns could reveal information about random output if not properly mitigated.
Modern QRNGs address this through shielding, self-testing, and real-time entropy validation.
Standardization and cost barriers also influence adoption.
While NIST and ISO frameworks define entropy validation methods, QRNG-specific standards are still emerging.
Meanwhile, hardware costs are falling, but they remain higher than traditional digital RNGs in large-scale deployments.
Where is QRNG technology heading next?
Quantum random number generators are evolving from specialized lab instruments to scalable, embedded technologies.
Recent breakthroughs are focused on improving speed, size, and verification. The same areas that define their path toward widespread adoption. Many of these advances directly address the engineering challenges discussed earlier, closing the gap between research prototypes and practical deployment.
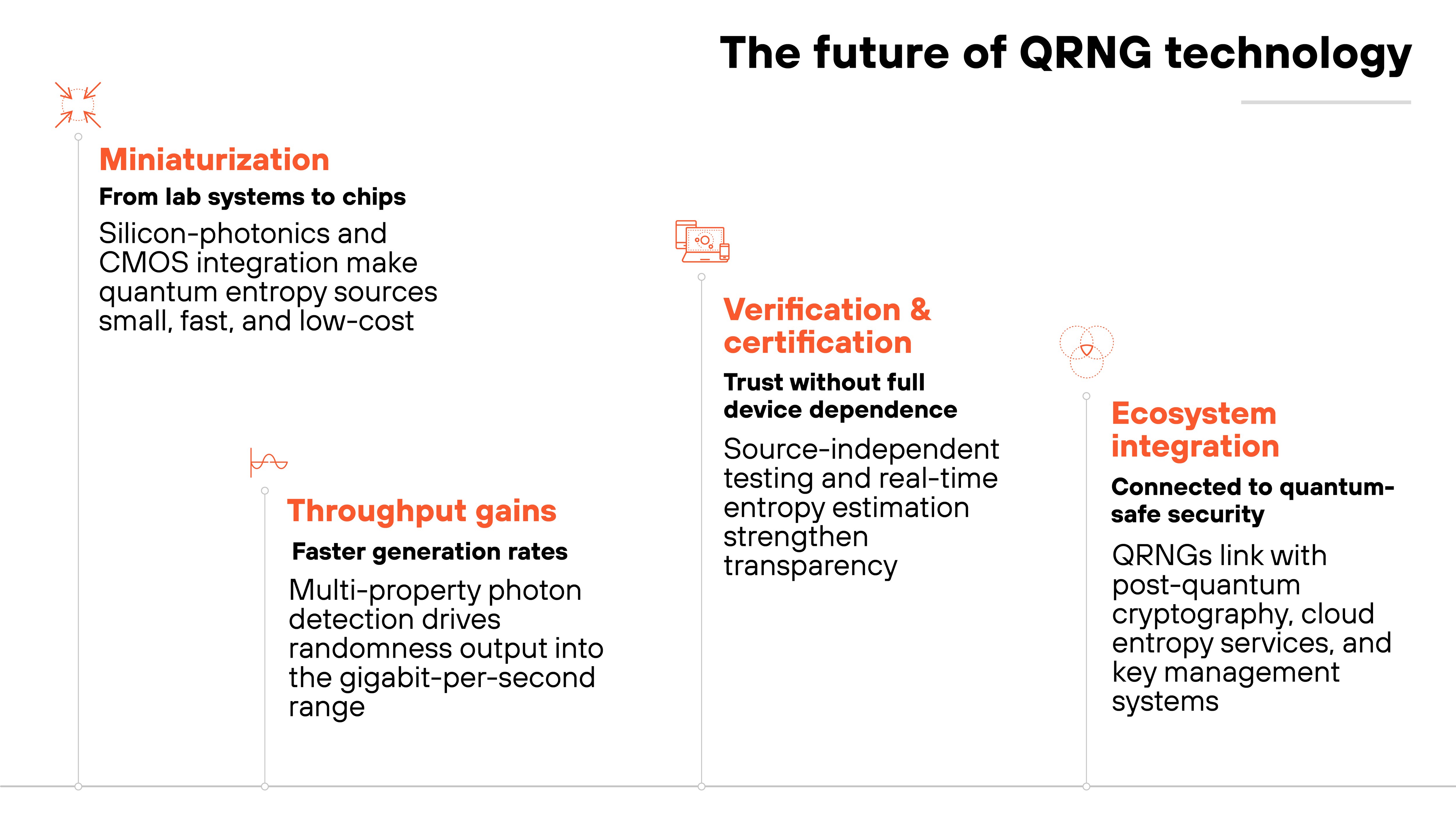
The most significant change is miniaturization.
Chip-based and CMOS-compatible QRNGs are now being developed using silicon photonics, allowing quantum entropy sources to be built directly into integrated circuits. This reduces cost and makes quantum-grade randomness feasible for mobile devices, IoT endpoints, and high-volume data center applications.
Another area of progress is throughput.
Researchers are advancing multi-dimensional photon detection, where multiple photon properties—such as phase, time, or polarization—are measured in parallel. This approach boosts generation rates into the gigabit-per-second range without compromising entropy quality.
Verification is improving too.
New source-independent certification techniques can validate quantum randomness even when parts of the device are untrusted. These methods combine self-testing and real-time entropy estimation, improving both transparency and assurance.
Integration with broader security ecosystems is also accelerating.
Researchers and vendors are exploring how QRNGs can connect with post-quantum cryptography frameworks, cloud-based entropy services, and quantum-safe key management systems. The goal is to make quantum randomness available wherever encryption, authentication, or trust decisions depend on it.
Ultimately, QRNGs are moving closer to the heart of digital security infrastructure. As quantum computing scales, QRNGs will secure not just algorithms but the randomness behind them.
